Curvature of the universe

The curvature is a quantity describing how the geometry of a space differs locally from the one of the flat space. The curvature of any locally isotropic space (and hence of a locally isotropic universe) falls into one of the three following cases:

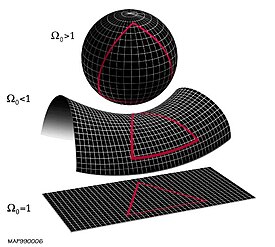
Zero curvature (flat); a drawn triangle's angles add up to 180° and the Pythagorean theorem holds; such 3-dimensional space is locally modeled by Euclidean space E³.Positive curvature; a drawn triangle's angles add up to more than 180°; such 3-dimensional space is locally modeled by a region of a 3-sphere S³.Negative curvature; a drawn triangle's angles add up to less than 180°; such 3-dimensional space is locally modeled by a region of a hyperbolic space H³.

Curved geometries are in the domain of Non-Euclidean geometry. An example of a positively curved space would be the surface of a sphere such as the Earth. A triangle drawn from the equator to a pole will have at least two angles equal 90°, which makes the sum of the 3 angles greater than 180°. An example of a negatively curved surface would be the shape of a saddle or mountain pass. A triangle drawn on a saddle surface will have the sum of the angles adding up to less than 180°.

The local geometry of the universe is determined by whether the density parameter Ω is greater than, less than, or equal to 1.
From top to bottom: a spherical universe with Ω > 1, a hyperbolic universe with Ω < 1, and a flat universe with Ω = 1. These depictions of two-dimensional surfaces are merely easily visualizable analogs to the 3-dimensional structure of (local) space.